In the last blog post, I discussed how polls do not account for variations that arise when sample results are extended to the population. I proposed that hypothesis testing and confidence intervals should be used in polls to enable stakeholders and the general public to assess the decisiveness of the results. While hypothesis testing gives a clear-cut answer on whether a poll can conclusively favour one side over the other, confidence intervals reveal the possibilities that might arise from a poll.
In this blog post, I used hypothesis testing and confidence intervals to analyse results from EU referendum polls in 2016. Using these techniques, I drew some interesting insights identifying polls that show a significant result and evaluated the usefulness of telephone polls compared to online ones.
Methodology
I collected a list of online and telephone British polls in 2016 from Wikipedia that surveyed people on how they would respond to the EU referendum question “Should the United Kingdom remain a member of the European Union or leave the European Union?”. I only included polls that had the raw numbers (not proportions) of people that would vote Remain or Leave in the referendum. These were required for calculating the proportion of the sample voting Remain or Leave to a high level of precision (to two decimal places) and to calculate the sample size (the total number of voters participating in the poll) which are used to calculate confidence intervals and p-values (see my previous blog post for more details). I collected weighted values from these polls as they make adjustments to create a nationally-represented sample of the UK.
From these polls, I excluded voters who were undecided or would refuse to vote for two reasons. Firstly, this reduces the number of possibilities to two (Remain or Leave) which enabled me to apply hypothesis testing and confidence intervals to a specific mutually-exclusive side. Secondly, on the day of the referendum, the count excludes anyone who is undecided or refused to vote when deciding whether the UK should Remain or Leave the EU. This can be simulated by excluding the number of voters who are undecided or refuse to vote. I then calculated p-values and confidence intervals of each poll according to the formulae from the last blog post.
Comparing statistical significance via z-values and confidence intervals
## Observations: 93 ## Variables: 15 ## $ poll_start <date> 2016-01-08, 2016-01-08, 2016-01-15, 2016-01-15, 20... ## $ poll_end <date> 2016-01-10, 2016-01-14, 2016-01-16, 2016-01-17, 20... ## $ pollster <chr> "ICM", "Panelbase", "Survation", "ICM", "ORB", "Com... ## $ poll_type <chr> "Online", "Online", "Online", "Online", "Online", "... ## $ num_remain <dbl> 901, 704, 368, 857, 1050, 544, 821, 289, 589, 664, ... ## $ num_leave <dbl> 778, 757, 392, 815, 965, 362, 826, 186, 569, 724, 7... ## $ total <dbl> 1679, 1461, 760, 1672, 2015, 906, 1647, 475, 1158, ... ## $ prop_leave <dbl> 0.4633711, 0.5181383, 0.5157895, 0.4874402, 0.47890... ## $ z_value <dbl> -3.00178625, 1.38659861, 0.87057150, -1.02714357, -... ## $ p_value <dbl> 2.684006e-03, 1.655642e-01, 3.839882e-01, 3.043529e... ## $ z_sig <chr> "Yes", "No", "No", "No", "Maybe", "Yes", "No", "Yes... ## $ error <dbl> 0.02385241, 0.02562212, 0.03553061, 0.02395912, 0.0... ## $ low_ci <dbl> 0.4395186, 0.4925161, 0.4802589, 0.4634811, 0.45709... ## $ high_ci <dbl> 0.4872235, 0.5437604, 0.5513201, 0.5113993, 0.50072... ## $ ci_sig <chr> "Yes", "No", "No", "No", "No", "Yes", "No", "Yes", ...
In total, 93 telephone and online polls were included in the analysis. Statistical significance can be determined by both the z-value which measures the deviation of the proportion of Leave voters from the null value of 50% (representing equal numbers of Remain and Leave voters) or via confidence intervals which depicts statistical significance by the confidence interval not crossing the 50% proportion threshold. I initially compared z-values and confidence intervals to see whether both techniques can similarly detect statistical significance at the p < 0.05 level.
## ## No Yes ## Maybe 4 1 ## No 54 0 ## Yes 0 34
The rows and columns in the table represent statistical significance detected by z-values and confidence intervals respectively. Overall, both techniques can identically delineate statistically significant and non-significant polls. I also included a “maybe” category for z-value hypothesis testing representing polls of borderline statistical significance (i.e., p-values between 0.05 and 0.10). Of these polls, four of them had a non-significant result as derived from confidence intervals.
We can visualise the comparison of statistical significance from z-values and confidence intervals:
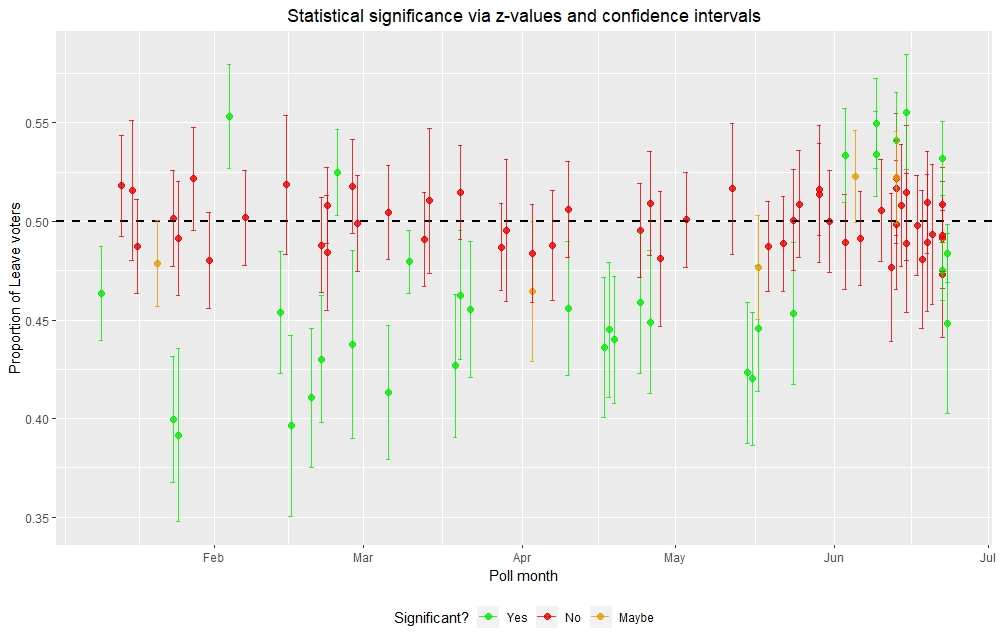
In general, polls that are statistically significant via z-values have confidence intervals that do not cross over the 50% threshold. In contrast, polls that are not statistically significant via z-values have confidence intervals that cross over the 50% threshold. Polls that are borderline statistically significant (represented by orange) had one end of the confidence interval “touching” or slightly crossing over the 50% threshold. This visualisation shows the ability of statistical techniques to distinguish polls that decisively favour one side from those that show a balance of votes between the two sides.
## ## No Yes ## Maybe 0.04 0.01 ## No 0.58 0.00 ## Yes 0.00 0.37
Most polls (58%) are not statistically significant with the proportion of Leave voters not deviating significantly from the 50% null value. These results suggest that these polls cannot decisively favour Leave over Remain and vice-versa. The remaining polls have a Leave result that is significantly (37%) or borderline (5%) different from the 50% null value.
Overall, these results underline that statistical significance derived from z-values and confidence intervals are equivalent to each other. Therefore, in subsequent analyses, I used statistical significance derived from z-values to investigate polling results further.
How can statistical significance assist in interpretability of polls?
I firstly counted the number of statistically significant and non-significant results from online and telephone polls.

From the graph, most non-statistically significant results come from online polls while most statistically significant results are derived from telephone polls. Identifying an interesting result, I investigated further at the characteristics of online and telephone polls in EU referendum polls.

Surprisingly, all telephone polls that had a statistically significant result favoured Remain as indicated by the lower than 50% proportion of Leave voters. They also had relatively small sample sizes, surveying less than 1,000 people. In contrast, most online polls, which survey more than 1,000 people, do not show a statistically significant result, describing a 50:50 split between Remain and Leave. Of the handful of online polls that are statistically significant, the number of online polls that favoured Leave (indicated by >50% Leave voters) is double that of those favouring Remain.

I also investigated the margins of error between online and telephone polls. Telephone polls had higher margins of error (median = 3.5%) compared to online polls (median = 2.4%) due to the smaller sample sizes. Given that the 2016 EU referendum favoured Leave over Remain, these results suggest that while online polls are more likely to be robust as they survey a larger sample size, telephone polls are more likely to declare a decisive result but are more prone to favour the wrong side. This might be one of the myriad of contributing factors why phone polls are more likely to get the EU referendum result wrong compared to online polls.
How do EU referendum polls track overtime?
I next looked at the polling results overtime and how they are affected by statistical significance, taking into consideration the poll type and sample size.

Most polls are not statistically significant, straddling along the 50% threshold. These polls suggest a 50:50 split between Remain and Leave voters, not favouring one side over the other. Of the polls that showed statistical significance, up until June nearly all of them are telephone polls that favoured Remain (indicated by lower than 50% Leave voters). There were only four online polls that showed statistically significant results with two favouring Remain and the other two favouring Leave. However, from June onwards, nearly all statistically significant results came from online polls. Most of them favoured Leave up until just before the referendum where the last two statistically significant online polls favoured Remain.
These online polls were different from the referendum result which favoured Leave over Remain. This is because there are other sources of error such as voter turnout that are not accounted for in the statistical techniques used. Nevertheless, hypothesis testing is a very powerful tool for limiting polls that show a decisive result from those that do not. This gives us a subset of the data from which insightful conclusions can be made.
Conclusion
Hypothesis testing is very useful for selecting polls that show a significant deviation from a 50:50 split between Remain and Leave voters. Combined with confidence intervals, these statistical techniques have unveiled some interesting results. For instance, while telephone polls are more likely to declare a decisive result, they are also more prone to favour the wrong side as can be seen in the 2016 EU referendum. In contrast, online polls are less likely to declare a decisive result but are more likely to favour the correct side due to surveying more people. It is why nearly all Brexit polls after the 2016 EU referendum are conducted online rathern than by phone.
In summary, the use of hypothesis testing and confidence intervals will serve to better clarify the usefulness of polls and whether they show a decisive result on a particular issue and what range of possibilities are available. Given the explosion of data and information in the modern age, it is more important than ever that people are equipped with the tools to interpret and assess the legitimacy and accuracy of facts. Teaching people how to use and interpret hypothesis tests and confidence intervals will serve them well for not only deciding whether they should care about a poll but also for assessing and debating findings from different sources of information.